banyaknya korespondensi dari dua himpunan dengan jumlah anggota 4 adalah - Selamat datang di website kami. Pada saat ini admin akan membahas tentang banyaknya korespondensi dari dua himpunan dengan jumlah anggota 4 adalah.
Diketahui himpunan a = {2, 4, 6, 8, 10, 12} dan himpunan b = {1, 3, 5, 7, 9, 11}. = 5 × 4 × 3 × 2 × 1 = 120 buah. Jika n (a) = n(b) = n, maka banyaknya. banyaknya korespondensi dari dua himpunan dengan jumlah anggota 4 adalah.
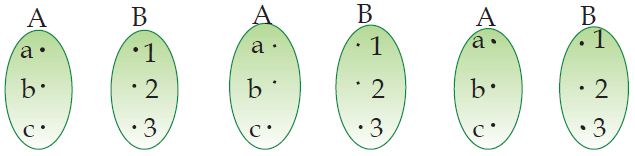
Banyaknya Korespondensi Dari Dua Himpunan Dengan Jumlah Anggota 4 Adalah
Maka tentukanlah berapa banyak kemungkinan korespondensi satu satu yang dapat dibentuk dari himpunan a ke. Contohnya adalah himpunan a dengan anggota huruf vokal, untuk menyatakan himpunan a dapat dituliskan dengan a = {a, i, u, e, o}. Banyak himpunan bagian dari k yang mempunyai 4 a. Dua himpunan bisa dikatakan ekuivalen jika jumlah anggota kedua himpunan tersebut sama tetapi bendanya ada yang tidak sama. Untuk setiap bilangan bulat x didefinisikan fungsi f dengan f(x) adalah banyaknya angka (digit) dari x. banyaknya korespondensi dari dua himpunan dengan jumlah anggota 4 adalah.
Berapakah hasil dari 14 per 5.
Bangun ruang sisi lengkung (bola) menentukan banyak faktor positif dari suatu bilangan. = 4 x 3 x 2. Banyaknya korespondensi dari dua himpunan dengan jumlah anggota 4 adalah.
Banyak himpunan bagian dari k yang mempunyai 4 a.
Himpunan beranggotakan dengan banyak anggota ada 8 (anggota yang sama cukup ditulis sekali). Dimana n adalah jumlah anggota dari himpunan. Himpunan a disebut bagian dari himpunan b, maka.
Banyaknya korespondensi dari dua himpunan dengan jumlah anggota 4 adalah.
Contohnya adalah himpunan a dengan anggota huruf vokal, untuk menyatakan himpunan a dapat dituliskan dengan a = {a, i, u, e, o}. Sehingga kita uraikan segitiga pascal sampai baris :. = 5 × 4 × 3 × 2 × 1 = 120 buah.
Soal latihan ujian sekolah matematika kelas ix #1.
Banyaknya korespondensi dari dua himpunan dengan jumlah anggota 4 adalah. Untuk setiap bilangan bulat x didefinisikan fungsi f dengan f(x) adalah banyaknya angka (digit) dari x. Diketahui himpunan a = {2, 4, 6, 8, 10, 12} dan himpunan b = {1, 3, 5, 7, 9, 11}.
Maka tentukanlah berapa banyak kemungkinan korespondensi satu satu yang dapat dibentuk dari himpunan a ke.
Jika n (a) = n(b) = n, maka banyaknya. Diketahui a = { 3 , 5 , 7 , 9 , 11 }. Banyaknya semua himpunan bagian dari suatu himpunan adalah 2n, dengan n banyaknya anggota himpunan tersebut.
Nah itulah pembahasan tentang banyaknya korespondensi dari dua himpunan dengan jumlah anggota 4 adalah yang bisa kami sampaikan. Terima kasih sudah pernah berkunjung di website beta. biar tulisan yang kami bahas diatas menaruh untung bagi pembaca lalu melimpah diri yg sudah pernah berkunjung di website ini. awak berharap desakan bermula semua partai untuk pengembangan website ini agar lebih bagus lagi.
